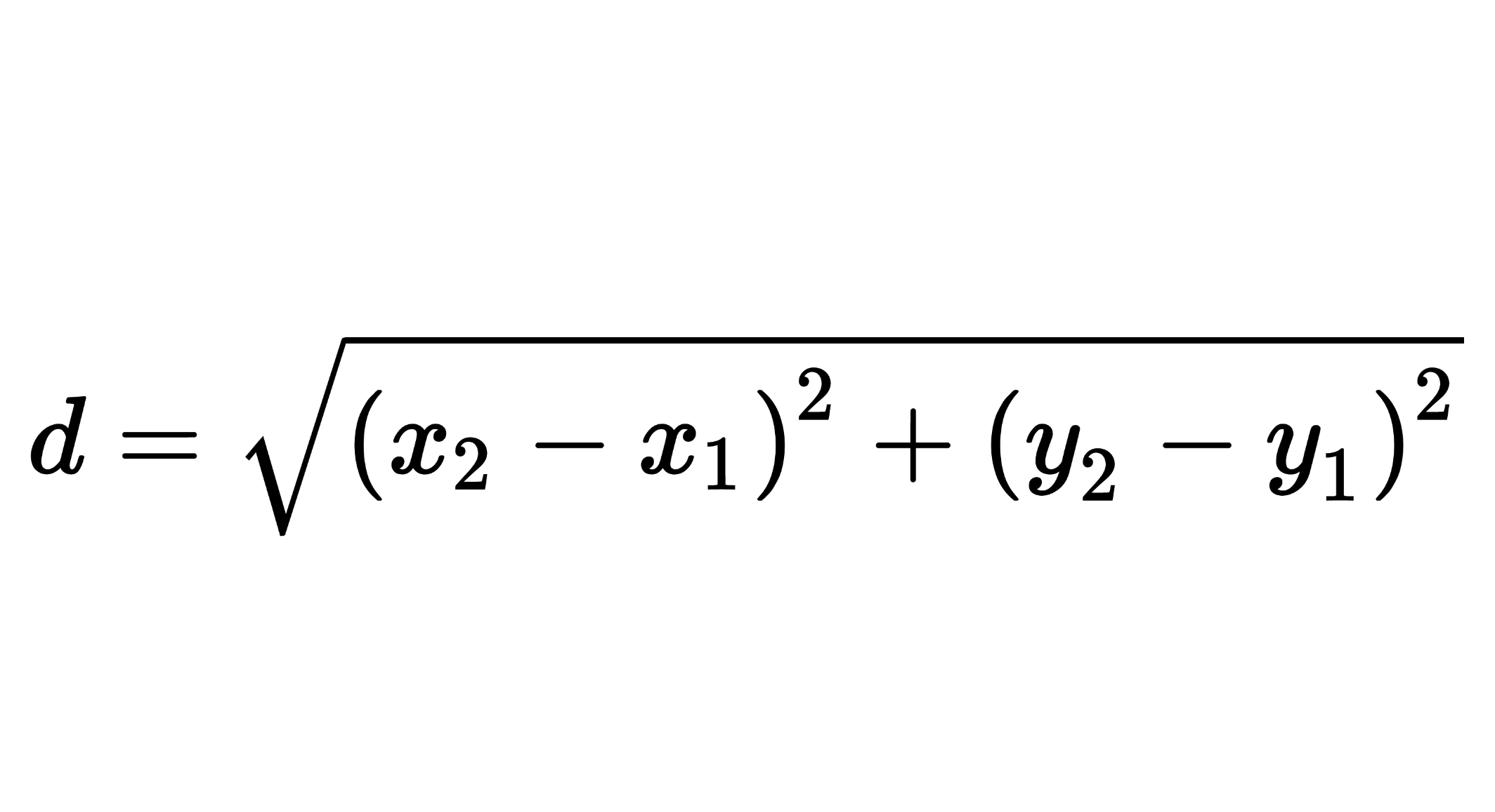
The built-in functions we have used, such as abs, pow, int, max, and range, have produced results. Calling each of these functions generates a value, which we usually assign to a variable or use as part of an expression.
biggest = max(3, 7, 2, 5)
x = abs(3 - 11) + 10We also wrote our own function to return the final amount for a compound interest calculation.
In this chapter, we are going to write more functions that return values, which we will call fruitful functions, for want of a better name. The first example is area, which returns the area of a circle with the given radius:
def area(radius):
b = 3.14159 * radius**2
return bWe have seen the return statement before, but in a fruitful function the return statement includes a return value. This statement means: evaluate the return expression, and then return it immediately as the result (the fruit) of this function. The expression provided can be arbitrarily complicated, so we could have written this function like this:
def area(radius):
return 3.14159 * radius * radiusOn the other hand, temporary variables like b above often make debugging easier.
Sometimes it is useful to have multiple return statements, one in each branch of a conditional. We have already seen the built-in abs, now we see how to write our own:
def absolute_value(x):
if x < 0:
return -x
else:
return xAnother way to write the above function is to leave out the else and just follow the if condition by the second return statement.
def absolute_value(x):
if x < 0:
return -x
return xThink about this version and convince yourself it works the same as the first one.
Code that appears after a return statement, or any other place the flow of execution can never reach, is called dead code, or unreachable code.
In a fruitful function, it is a good idea to ensure that every possible path through the program hits a return statement. The following version of absolute_value fails to do this:
def bad_absolute_value(x):
if x < 0:
return -x
elif x > 0:
return xThis version is not correct because if x happens to be 0, neither condition is true, and the function ends without hitting a return statement. In this case, the return value is a special value called None:
>>> print(bad_absolute_value(0))
NoneAll Python functions return None whenever they do not return another value.
It is also possible to use a return statement in the middle of a for loop, in which case control immediately returns from the function. Let us assume that we want a function which looks through a list of words. It should return the first 2-letter word. If there is not one, it should return the empty string:
def find_first_2_letter_word(xs):
for wd in xs:
if len(wd) == 2:
return wd
return "">>> find_first_2_letter_word(["This", "is", "a", "dead", "parrot"])
'is'
>>> find_first_2_letter_word(["I", "like", "cheese"])
''Single-step through this code and convince yourself that in the first test case that we’ve provided, the function returns while processing the second element in the list: it does not have to traverse the whole list.
At this point, you should be able to look at complete functions and tell what they do. Also, if you have been doing the exercises, you have written some small functions. As you write larger functions, you might start to have more difficulty, especially with runtime and semantic errors.
To deal with increasingly complex programs, we are going to suggest a technique called incremental development. The goal of incremental development is to avoid long debugging sessions by adding and testing only a small amount of code at a time.
As an example, suppose we want to find the distance between two points, given by the coordinates (x1, y1) and (x2, y2). By the Pythagorean theorem, the distance is:
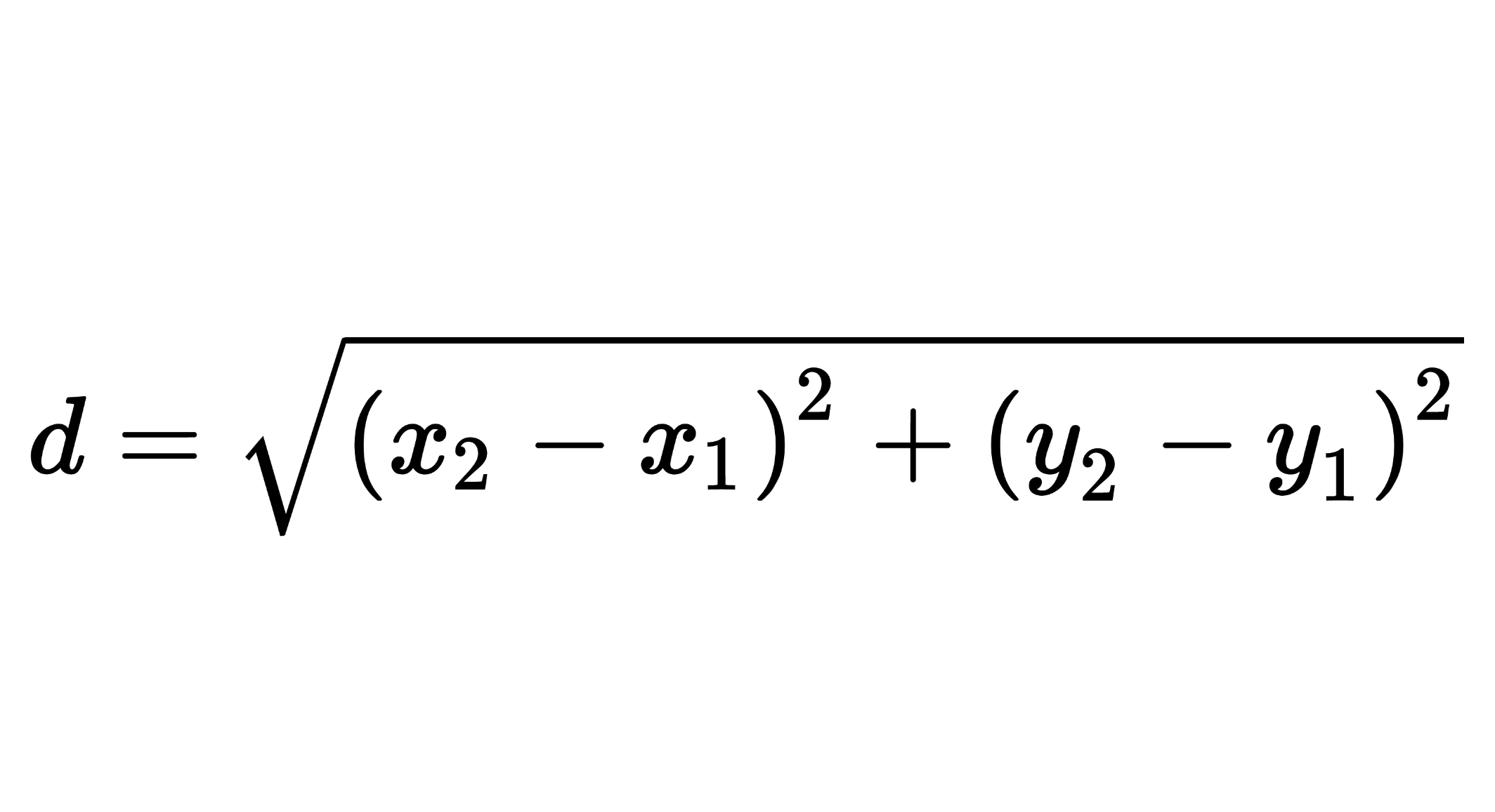
The first step is to consider what a distance function should look like in Python. In other words, what are the inputs (parameters) and what is the output (return value)?
In this case, the two points are the inputs, which we can represent using four parameters. The return value is the distance, which is a floating-point value.
Already we can write an outline of the function that captures our thinking so far:
def distance(x1, y1, x2, y2):
return 0.0Obviously, this version of the function doesn’t compute distances; it always returns zero. But it is syntactically correct, and it will run, which means that we can test it before we make it more complicated.
To test the new function, we call it with sample values:
>>> distance(1, 2, 4, 6)
0.0We chose these values so that the horizontal distance equals 3 and the vertical distance equals 4; that way, the result is 5 (the hypotenuse of a 3-4-5 triangle). When testing a function, it is useful to know the right answer.
At this point we have confirmed that the function is syntactically correct, and we can start adding lines of code. After each incremental change, we test the function again. If an error occurs at any point, we know where it must be — in the last line we added.
A logical first step in the computation is to find the differences x2- x1 and y2- y1. We will refer to those values using temporary variables named dx and dy.
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
return 0.0If we call the function with the arguments shown above, when the flow of execution gets to the return statement, dx should be 3 and dy should be 4. We can check that this is the case in PyScripter by putting the cursor on the return statement, and running the program to break execution when it gets to the cursor (using the F4 key). Then we inspect the variables dx and dy by hovering the mouse above them, to confirm that the function is getting the right parameters and performing the first computation correctly. If not, there are only a few lines to check.
Next we compute the sum of squares of dx and dy:
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
dsquared = dx*dx + dy*dy
return 0.0Again, we could run the program at this stage and check the value of dsquared (which should be 25).
Finally, using the fractional exponent 0.5 to find the square root, we compute and return the result:
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
dsquared = dx*dx + dy*dy
result = dsquared**0.5
return resultIf that works correctly, you are done. Otherwise, you might want to inspect the value of result before the return statement.
When you start out, you might add only a line or two of code at a time. As you gain more experience, you might find yourself writing and debugging bigger conceptual chunks. Either way, stepping through your code one line at a time and verifying that each step matches your expectations can save you a lot of debugging time. As you improve your programming skills you should find yourself managing bigger and bigger chunks: this is very similar to the way we learned to read letters, syllables, words, phrases, sentences, paragraphs, etc., or the way we learn to chunk music — from individual notes to chords, bars, phrases, and so on.
The key aspects of the process are:
Start with a working skeleton program and make small incremental changes. At any point, if there is an error, you will know exactly where it is.
Use temporary variables to refer to intermediate values so that you can easily inspect and check them.
Once the program is working, relax, sit back, and play around with your options. (There is interesting research that links “playfulness” to better understanding, better learning, more enjoyment, and a more positive mindset about what you can achieve — so spend some time fiddling around!) You might want to consolidate multiple statements into one bigger compound expression, or rename the variables you’ve used, or see if you can make the function shorter. A good guideline is to aim for making code as easy as possible for others to read.
Here is another version of the function. It makes use of a square root function that is in the math module (we’ll learn about modules shortly). Which do you prefer? Which looks “closer” to the Pythagorean formula we started out with?
import math
def distance(x1, y1, x2, y2):
return math.sqrt( (x2-x1)**2 + (y2-y1)**2 )>>> distance(1, 2, 4, 6)
5.0Another powerful technique for debugging (an alternative to single-stepping and inspection of program variables), is to insert extra print functions in carefully selected places in your code. Then, by inspecting the output of the program, you can check whether the algorithm is doing what you expect it to. Be clear about the following, however:
You must have a clear solution to the problem, and must know what should happen before you can debug a program. Work on solving the problem on a piece of paper (perhaps using a flowchart to record the steps you take) before you concern yourself with writing code. Writing a program doesn’t solve the problem — it simply automates the manual steps you would take. So first make sure you have a pen-and-paper manual solution that works. Programming then is about making those manual steps happen automatically.
Do not write chatterbox functions. A chatterbox is a fruitful function that, in addition to its primary task, also asks the user for input, or prints output, when it would be more useful if it simply shut up and did its work quietly.
For example, we’ve seen built-in functions like range, max and abs. None of these would be useful building blocks for other programs if they prompted the user for input, or printed their results while they performed their tasks.
So a good tip is to avoid calling print and input functions inside fruitful functions, unless the primary purpose of your function is to perform input and output. The one exception to this rule might be to temporarily sprinkle some calls to print into your code to help debug and understand what is happening when the code runs, but these will then be removed once you get things working.
As you should expect by now, you can call one function from within another. This ability is called composition.
As an example, we’ll write a function that takes two points, the center of the circle and a point on the perimeter, and computes the area of the circle.
Assume that the center point is stored in the variables xc and yc, and the perimeter point is in xp and yp. The first step is to find the radius of the circle, which is the distance between the two points. Fortunately, we’ve just written a function, distance, that does just that, so now all we have to do is use it:
radius = distance(xc, yc, xp, yp)The second step is to find the area of a circle with that radius and return it. Again we will use one of our earlier functions:
result = area(radius)
return resultWrapping that up in a function, we get:
def area2(xc, yc, xp, yp):
radius = distance(xc, yc, xp, yp)
result = area(radius)
return resultWe called this function area2 to distinguish it from the area function defined earlier.
The temporary variables radius and result are useful for development, debugging, and single-stepping through the code to inspect what is happening, but once the program is working, we can make it more concise by composing the function calls:
def area2(xc, yc, xp, yp):
return area(distance(xc, yc, xp, yp))Functions can return Boolean values, which is often convenient for hiding complicated tests inside functions. For example:
def is_divisible(x, y):
""" Test if x is exactly divisible by y """
if x % y == 0:
return True
else:
return FalseIt is common to give Boolean functions names that sound like yes/no questions. is_divisible returns either True or False to indicate whether the x is or is not divisible by y.
We can make the function more concise by taking advantage of the fact that the condition of the if statement is itself a Boolean expression. We can return it directly, avoiding the if statement altogether:
def is_divisible(x, y):
return x % y == 0This session shows the new function in action:
>>> is_divisible(6, 4)
False
>>> is_divisible(6, 3)
TrueBoolean functions are often used in conditional statements:
if is_divisible(x, y):
... # Do something ...
else:
... # Do something else ...It might be tempting to write something like:
if is_divisible(x, y) == True:but the extra comparison is unnecessary.
Readability is very important to programmers, since in practice programs are read and modified far more often then they are written. But, like most rules, we occasionally break them. Most of the code examples in this book will be consistent with the Python Enhancement Proposal 8 (PEP 8), a style guide developed by the Python community.
We’ll have more to say about style as our programs become more complex, but a few pointers will be helpful already:
It is a common best practice in software development to include automatic unit testing of source code. Unit testing provides a way to automatically verify that individual pieces of code, such as functions, are working properly. This makes it possible to change the implementation of a function at a later time and quickly test that it still does what it was intended to do.
Some years back organizations had the view that their valuable asset was the program code and documentation. Organizations will now spend a large portion of their software budgets on crafting (and preserving) their tests.
Unit testing also forces the programmer to think about the different cases that the function needs to handle. You also only have to type the tests once into the script, rather than having to keep entering the same test data over and over as you develop your code.
Extra code in your program which is there because it makes debugging or testing easier is called scaffolding.
A collection of tests for some code is called its test suite.
There are a few different ways to do unit testing in Python — but at this stage we’re going to ignore what the Python community usually does, and we’re going to start with two functions that we’ll write ourselves. We’ll use these for writing our unit tests.
Let’s start with the absolute_value function that we wrote earlier in this chapter. Recall that we wrote a few different versions, the last of which was incorrect, and had a bug. Would tests have caught this bug?
First we plan our tests. We’d like to know if the function returns the correct value when its argument is negative, or when its argument is positive, or when its argument is zero. When planning your tests, you’ll always want to think carefully about the “edge” cases — here, an argument of 0 to absolute_value is on the edge of where the function behaviour changes, and as we saw at the beginning of the chapter, it is an easy spot for the programmer to make a mistake! So it is a good case to include in our test suite.
We’re going to write a helper function for checking the results of one test. It takes a boolean argument and will either print a message telling us that the test passed, or it will print a message to inform us that the test failed. The first line of the body (after the function’s docstring) magically determines the line number in the script where the call was made from. This allows us to print the line number of the test, which will help when we want to identify which tests have passed or failed.
import sys
def test(did_pass):
""" Print the result of a test. """
linenum = sys._getframe(1).f_lineno # Get the caller's line number.
if did_pass:
msg = "Test at line {0} ok.".format(linenum)
else:
msg = "Test at line {0} FAILED.".format(linenum)
print(msg)There is also some slightly tricky string formatting using the format method which we will gloss over for the moment, and cover in detail in a future chapter. But with this function written, we can proceed to construct our test suite:
def test_suite():
""" Run the suite of tests for code in this module (this file).
"""
test(absolute_value(17) == 17)
test(absolute_value(-17) == 17)
test(absolute_value(0) == 0)
test(absolute_value(3.14) == 3.14)
test(absolute_value(-3.14) == 3.14)
test_suite() # Here is the call to run the testsHere you’ll see that we’ve constructed five tests in our test suite. We could run this against the first or second versions (the correct versions) of absolute_value, and we’d get output similar to the following:
Test at line 25 ok.
Test at line 26 ok.
Test at line 27 ok.
Test at line 28 ok.
Test at line 29 ok.But let’s say you change the function to an incorrect version like this:
def absolute_value(n): # Buggy version
""" Compute the absolute value of n """
if n < 0:
return 1
elif n > 0:
return nCan you find at least two mistakes in this code? Our test suite can! We get:
Test at line 25 ok.
Test at line 26 FAILED.
Test at line 27 FAILED.
Test at line 28 ok.
Test at line 29 FAILED.These are three examples of failing tests.
There is a built-in Python statement called assert that does almost the same as our test function (except the program stops when the first assertion fails). You may want to read about it, and use it instead of our test function.
Boolean function
A function that returns a Boolean value. The only possible values of the bool type are False and True.
chatterbox function
A function which interacts with the user (using input or print) when it should not. Silent functions that just convert their input arguments into their output results are usually the most useful ones.
composition (of functions)
Calling one function from within the body of another, or using the return value of one function as an argument to the call of another.
dead code
Part of a program that can never be executed, often because it appears after a return statement.
fruitful function
A function that yields a return value instead of None.
incremental development
A program development plan intended to simplify debugging by adding and testing only a small amount of code at a time.
None
A special Python value. One use in Python is that it is returned by functions that do not execute a return statement with a return argument.
return value
The value provided as the result of a function call.
scaffolding
Code that is used during program development to assist with development and debugging. The unit test code that we added in this chapter are examples of scaffolding.
temporary variable
A variable used to store an intermediate value in a complex calculation.
test suite
A collection of tests for some code you have written.
unit testing
An automatic procedure used to validate that individual units of code are working properly. Having a test suite is extremely useful when somebody modifies or extends the code: it provides a safety net against going backwards by putting new bugs into previously working code. The term regression testing is often used to capture this idea that we don’t want to go backwards!
All of the exercises below should be added to a single file. In that file, you should also add the test and test_suite scaffolding functions shown above, and then, as you work through the exercises, add the new tests to your test suite. (If you open the online version of the textbook, you can easily copy and paste the tests and the fragments of code into your Python editor.)
After completing each exercise, confirm that all the tests pass.
The four compass points can be abbreviated by single-letter strings as “N”, “E”, “S”, and “W”. Write a function turn_clockwise that takes one of these four compass points as its parameter, and returns the next compass point in the clockwise direction. Here are some tests that should pass:
test(turn_clockwise("N") == "E")
test(turn_clockwise("W") == "N")You might ask “What if the argument to the function is some other value?” For all other cases, the function should return the value None:
test(turn_clockwise(42) == None)
test(turn_clockwise("rubbish") == None)Write a function day_name that converts an integer number 0 to 6 into the name of a day. Assume day 0 is “Sunday”. Once again, return None if the arguments to the function are not valid. Here are some tests that should pass:
test(day_name(3) == "Wednesday")
test(day_name(6) == "Saturday")
test(day_name(42) == None)Write the inverse function day_num which is given a day name, and returns its number:
test(day_num("Friday") == 5)
test(day_num("Sunday") == 0)
test(day_num(day_name(3)) == 3)
test(day_name(day_num("Thursday")) == "Thursday")Once again, if this function is given an invalid argument, it should return None:
test(day_num("Halloween") == None)Write a function that helps answer questions like ‘“Today is Wednesday. I leave on holiday in 19 days time. What day will that be?”’ So the function must take a day name and a delta argument — the number of days to add — and should return the resulting day name:
test(day_add("Monday", 4) == "Friday")
test(day_add("Tuesday", 0) == "Tuesday")
test(day_add("Tuesday", 14) == "Tuesday")
test(day_add("Sunday", 100) == "Tuesday")Hint: use the first two functions written above to help you write this one.
Can your day_add function already work with negative deltas? For example, -1 would be yesterday, or -7 would be a week ago:
test(day_add("Sunday", -1) == "Saturday")
test(day_add("Sunday", -7) == "Sunday")
test(day_add("Tuesday", -100) == "Sunday")If your function already works, explain why. If it does not work, make it work.
Hint: Play with some cases of using the modulus function % (introduced at the beginning of the previous chapter). Specifically, explore what happens to x % 7 when x is negative.
Write a function days_in_month which takes the name of a month, and returns the number of days in the month. Ignore leap years:
test(days_in_month("February") == 28)
test(days_in_month("December") == 31)If the function is given invalid arguments, it should return None.
Write a function to_secs that converts hours, minutes and seconds to a total number of seconds. Here are some tests that should pass:
test(to_secs(2, 30, 10) == 9010)
test(to_secs(2, 0, 0) == 7200)
test(to_secs(0, 2, 0) == 120)
test(to_secs(0, 0, 42) == 42)
test(to_secs(0, -10, 10) == -590)Extend to_secs so that it can cope with real values as inputs. It should always return an integer number of seconds (truncated towards zero):
test(to_secs(2.5, 0, 10.71) == 9010)
test(to_secs(2.433,0,0) == 8758)Write three functions that are the “inverses” of to_secs:
hours_in returns the whole integer number of hours represented by a total number of seconds.
minutes_in returns the whole integer number of left over minutes in a total number of seconds, once the hours have been taken out.
seconds_in returns the left over seconds represented by a total number of seconds.
You may assume that the total number of seconds passed to these functions is an integer. Here are some test cases:
test(hours_in(9010) == 2)
test(minutes_in(9010) == 30)
test(seconds_in(9010) == 10)It won’t always be obvious what is wanted …
In the third case above, the requirement seems quite ambiguous and fuzzy. But the test clarifies what we actually need to do.
Unit tests often have this secondary benefit of clarifying the specifications. If you write your own test suites, consider it part of the problem-solving process as you ask questions about what you really expect to happen, and whether you’ve considered all the possible cases.
Given our emphasis on thinking like a computer scientist, you might enjoy reading at least one reference about thinking, and about fun ideas like fluid intelligence, a key ingredient in problem solving. See, for example, http://psychology.about.com/od/cognitivepsychology/a/fluid-crystal.htm. Learning Computer Science requires a good mix of both fluid and crystallized kinds of intelligence.
Which of these tests fail? Explain why.
test(3 % 4 == 0)
test(3 % 4 == 3)
test(3 / 4 == 0)
test(3 // 4 == 0)
test(3+4 * 2 == 14)
test(4-2+2 == 0)
test(len("hello, world!") == 13)Write a compare function that returns 1 if a > b, 0 if a == b, and -1 if a < b
test(compare(5, 4) == 1)
test(compare(7, 7) == 0)
test(compare(2, 3) == -1)
test(compare(42, 1) == 1)Write a function called hypotenuse that returns the length of the hypotenuse of a right triangle given the lengths of the two legs as parameters:
test(hypotenuse(3, 4) == 5.0)
test(hypotenuse(12, 5) == 13.0)
test(hypotenuse(24, 7) == 25.0)
test(hypotenuse(9, 12) == 15.0)Write a function slope(x1, y1, x2, y2) that returns the slope of the line through the points (x1, y1) and (x2, y2). Be sure your implementation of slope can pass the following tests:
test(slope(5, 3, 4, 2) == 1.0)
test(slope(1, 2, 3, 2) == 0.0)
test(slope(1, 2, 3, 3) == 0.5)
test(slope(2, 4, 1, 2) == 2.0)Then use a call to slope in a new function named intercept(x1, y1, x2, y2) that returns the y-intercept of the line through the points (x1, y1) and (x2, y2)
test(intercept(1, 6, 3, 12) == 3.0)
test(intercept(6, 1, 1, 6) == 7.0)
test(intercept(4, 6, 12, 8) == 5.0)Write a function called is_even(n) that takes an integer as an argument and returns True if the argument is an even number and False if it is odd.
Add your own tests to the test suite.
Now write the function is_odd(n) that returns True when n is odd and False otherwise. Include unit tests for this function too.
Finally, modify it so that it uses a call to is_even to determine if its argument is an odd integer, and ensure that its test still pass.
Write a function is_factor(f, n) that passes these tests:
test(is_factor(3, 12))
test(not is_factor(5, 12))
test(is_factor(7, 14))
test(not is_factor(7, 15))
test(is_factor(1, 15))
test(is_factor(15, 15))
test(not is_factor(25, 15))An important role of unit tests is that they can also act as unambiguous “specifications” of what is expected. These test cases answer the question “Do we treat 1 and 15 as factors of 15”?
Write is_multiple to satisfy these unit tests:
test(is_multiple(12, 3))
test(is_multiple(12, 4))
test(not is_multiple(12, 5))
test(is_multiple(12, 6))
test(not is_multiple(12, 7))Can you find a way to use is_factor in your definition of is_multiple?
Write the function f2c(t) designed to return the integer value of the nearest degree Celsius for given temperature in Fahrenheit. (hint: you may want to make use of the built-in function, round. Try printing round.__doc__ in a Python shell or looking up help for the round function, and experimenting with it until you are comfortable with how it works.)
test(f2c(212) == 100) # Boiling point of water
test(f2c(32) == 0) # Freezing point of water
test(f2c(-40) == -40) # Wow, what an interesting case!
test(f2c(36) == 2)
test(f2c(37) == 3)
test(f2c(38) == 3)
test(f2c(39) == 4)Now do the opposite: write the function c2f which converts Celsius to Fahrenheit:
test(c2f(0) == 32)
test(c2f(100) == 212)
test(c2f(-40) == -40)
test(c2f(12) == 54)
test(c2f(18) == 64)
test(c2f(-48) == -54)